Find Leaves of Binary Tree

Patrick Leaton
Published: July 5, 2021, 7:51 p.m.
Problem Description

Given the root of a binary tree, collect a tree's nodes as if you were doing this:
  • Collect all the leaf nodes.
  • Remove all the leaf nodes.
  • Repeat until the tree is empty.
 
Example 1:
Input: root = [1,2,3,4,5]
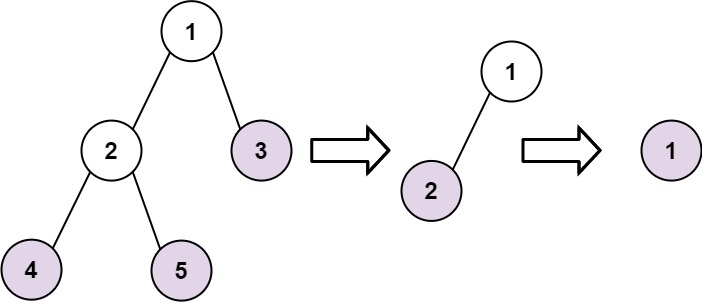
Output: [[4,5,3],[2],[1]]
Explanation:
[[3,5,4],[2],[1]] and [[3,4,5],[2],[1]] are also considered correct answers since per each level it does not matter the order on which elements are returned.
Example 2:
Input: root = [1]
Output: [[1]]
 
Constraints:
  • The number of nodes in the tree is in the range [1, 100].
  • -100 <= Node.val <= 100
 
The description was taken from https://leetcode.com/problems/find-leaves-of-binary-tree/.

Problem Solution

#O(N) Time, O(N) Space
class Solution:
    def findLeaves(self, root: TreeNode) -> List[List[int]]:
        layers = {}
       
        def dfs(node: TreeNode, height: int) -> int:
            if not node:
                return height
 
            left = dfs(node.left, height)
            right = dfs(node.right, height)
            height = max(left, right) + 1
 
            if height not in layers:
                layers[height] = [node.val]
            else:
                layers[height].append(node.val)
 
            node.left = node.right = None
            return height
       
        dfs(root, 0)
        return layers.values()

Problem Explanation

With Binary Tree questions, it is important to ask, "whose information do we need first?".  

This will let us know whether to perform an inorder, preorder, or postorder traversal.

For any questions involving height, they are almost always going to require a postorder traversal so that each child node is visited before their parent.  This is because, in order for us to know what the height of a node is, we will need to know the height of each child node beneath it.

A node's height isn't how far it is from the root, but how many nodes are stacked under it, and a leaf node is a node with a height of one.

To solve this question, we can perform a postorder Depth-First Search and calculate the height of each node, then use that height as a  key to group each node by their heights within a HashMap we will build.  

Once we have calculated the height of a node, we will set its children as null so that we can remove them.

When we have finished traversing the tree, we will return the groupings of the height dictionary.

Let's start by creating our layers hashmap that we will use to keep the order of which nodes belong to which height.

        layers = {}

Then, we will create our recursive, dfs function that will require a node and a height value as arguments.

        def dfs(node: TreeNode, height: int) -> int:

 

Being a recursive function, let's make sure we set the base case right away.

The base case is if we have reached a null node, then we have reached the end of a dfs path, which is the bottom of a tree branch.

If that is the case, we will return the same height that was passed to this root node and return from this DFS path so we can begin crawling back up the tree.

            if not node:
                return height

 

We'll recurse the left and right branches of the tree, and once we find out what their heights are, we will add one to the max height between them.  That will be the height of the current function call's node.

We take the max between them because if we had two children on one branch and one child on the other, we would be as tall as the two children, plus ourselves.

            left = dfs(node.left, height)
            right = dfs(node.right, height)
            height = max(left, right) + 1

 

After we get our height, we will append our node value to the layers dictionary, then set both children to none so that we can remove them.

            if height not in layers:
                layers[height] = [node.val]
            else:
                layers[height].append(node.val)
 
            node.left = node.right = None

 

Once we have done that, we will crawl up and do the same for this node's parent until we have finished with the root.

            return height

Now that we have the DFS function built, we will make the initial call with the root and an empty height value.

        dfs(root, 0)

 

We'll finally return the nodes in the layers dictionary, grouped by their respective heights.

        return layers.values()