Problem Description
Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:
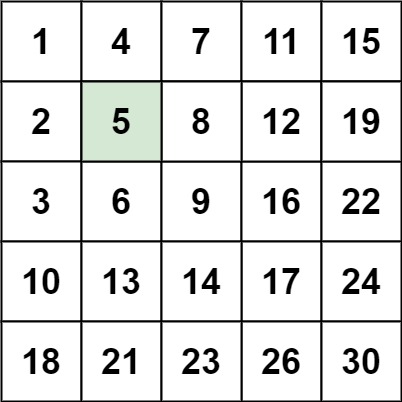
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 Output: true
Example 2:
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-10^9 <= matix[i][j] <= 10^9- All the integers in each row are sorted in ascending order.
- All the integers in each column are sorted in ascending order.
-10^9 <= target <= 10^9
The description was taken from https://leetcode.com/problems/search-a-2d-matrix-ii/.
Problem Solution
#O(N+M) Time, O(1) Spaceclass Solution: def searchMatrix(self, matrix: List[List[int]], target: int) -> bool: m, n = len(matrix[0]), len(matrix) row, col = 0, m-1 if n == 0 or m == 0: return False while row < n and col >= 0: if matrix[row][col] == target: return True if matrix[row][col] < target: row += 1 else: col -= 1 return FalseProblem Explanation
The way the matrices are set up is pretty funky.
This is because we wouldn't be able to flatten the matrix into a single sorted array. Because of that, a normal binary search won't work. However, that doesn't mean we can't still reduce the search space within each iteration to move from an O(Log(N*M)) solution to an O(Log(N+M)) solution.
What we will do is perform a binary search but only on the rows and columns without comparing a mean value to the target. Instead, we will see if our current element is less than the target, if it is then we will skip the rest of the row. If it is not, then we will skip the rest of the column. We will do this until we land right on the target, and if that never happens then the target doesn't exist.
This won't eliminate the search space by half within each iteration as a normal binary search would, but it will still eliminate the search space by one row or column within each iteration.
Let's start by getting a count of how many columns and rows we have so that we know where our search bounds are.
m, n = len(matrix[0]), len(matrix)
Next, we will set our row pointer to the first row, and our column pointer to the last column.
row, col = 0, m-1
If we have zero rows or zero columns, we will have a matrix of size zero since the product of anything multiplied by zero will be zero.
If we have no matrix, we can't find any target.
if n == 0 or m == 0: return False
Same as most binary search algorithms, we will continue our iterations until our pointers have reduced the search space to zero, meaning they overlapped and went outside the bounds of the data structure.
while row < n and col >= 0:
If the current element equals the target, we have found the target so we will return true.
if matrix[row][col] == target: return True
If the current element is less than the target, we will skip this row.
if matrix[row][col] < target: row += 1
If the current element is greater than the target, we will skip this column.
else: col -= 1
If we have reduced the search space to zero from our row and column pointers overlapping, we will return false since we searched everywhere and didn't find the target.
Let's go ahead and draw out what this search space reduction will look like with the the matrix being [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], and the target being 5.
| 1 | 4 | 7 | 11 | 15 |
| 2 | 5 | 8 | 12 | 19 |
| 3 | 6 | 9 | 16 | 22 |
| 10 | 13 | 14 | 17 | 24 |
| 18 | 21 | 23 | 26 | 30 |
We set our pointers to the first row and the last column, we are looking for five.
We compare the current element, matrix[row][col] against the target.
| 1 | 4 | 7 | 11 | 15 |
| 2 | 5 | 8 | 12 | 19 |
| 3 | 6 | 9 | 16 | 22 |
| 10 | 13 | 14 | 17 | 24 |
| 18 | 21 | 23 | 26 | 30 |
The current value is lower, skip this row.
| 1 | 4 | 7 | 11 | 15 |
| 2 | 5 | 8 | 12 | 19 |
| 3 | 6 | 9 | 16 | 22 |
| 10 | 13 | 14 | 17 | 24 |
| 18 | 21 | 23 | 26 | 30 |
Compare the next two values.
| 1 | 4 | 7 | 11 | 15 |
| 2 | 5 | 8 | 12 | 19 |
| 3 | 6 | 9 | 16 | 22 |
| 10 | 13 | 14 | 17 | 24 |
| 18 | 21 | 23 | 26 | 30 |
The current value is greater, skip this column.
| 1 | 4 | 7 | 11 | 15 |
| 2 | 5 | 8 | 12 | 19 |
| 3 | 6 | 9 | 16 | 22 |
| 10 | 13 | 14 | 17 | 24 |
| 18 | 21 | 23 | 26 | 30 |
Compare the next two values.
| 1 | 4 | 7 | 11 | 15 |
| 2 | 5 | 8 | 12 | 19 |
| 3 | 6 | 9 | 16 | 22 |
| 10 | 13 | 14 | 17 | 24 |
| 18 | 21 | 23 | 26 | 30 |
The current value is greater, skip this column.
| 1 | 4 | 7 | 11 | 15 |
| 2 | 5 | 8 | 12 | 19 |
| 3 | 6 | 9 | 16 | 22 |
| 10 | 13 | 14 | 17 | 24 |
| 18 | 21 | 23 | 26 | 30 |
Compare the next two values.
| 1 | 4 | 7 | 11 | 15 |
| 2 | 5 | 8 | 12 | 19 |
| 3 | 6 | 9 | 16 | 22 |
| 10 | 13 | 14 | 17 | 24 |
| 18 | 21 | 23 | 26 | 30 |
The current value is greater, skip this column.
| 1 | 4 | 7 | 11 | 15 |
| 2 | 5 | 8 | 12 | 19 |
| 3 | 6 | 9 | 16 | 22 |
| 10 | 13 | 14 | 17 | 24 |
| 18 | 21 | 23 | 26 | 30 |
Compare the next two values.
| 1 | 4 | 7 | 11 | 15 |
| 2 | 5 | 8 | 12 | 19 |
| 3 | 6 | 9 | 16 | 22 |
| 10 | 13 | 14 | 17 | 24 |
| 18 | 21 | 23 | 26 | 30 |
They are equal, return true.
If the target wasn't in the matrix, the entire thing would end up black and we'd return false.