Problem Description
Given a binary tree
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Follow up:
- You may only use constant extra space.
- Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.
Example 1:
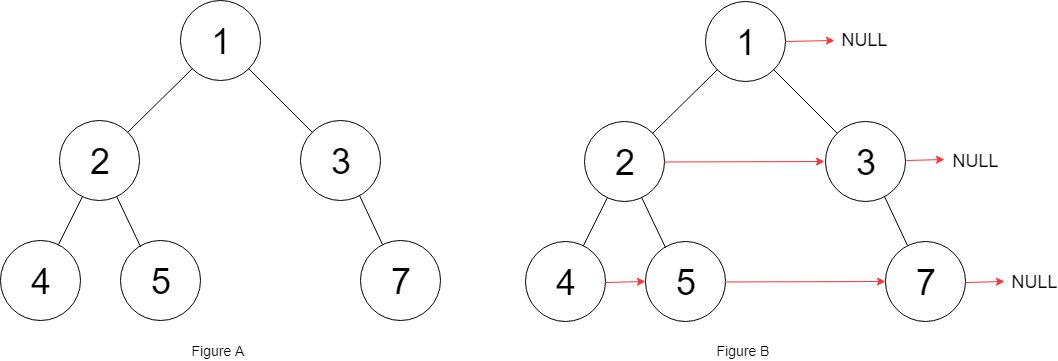
Input: root = [1,2,3,4,5,null,7] Output: [1,#,2,3,#,4,5,7,#] Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
Constraints:
- The number of nodes in the given tree is less than
6000. -100 <= node.val <= 100
The description was taken from https://leetcode.com/problems/populating-next-right-pointers-in-each-node-ii/.
Problem Solution
#Iterative BFS#O(N) Time, O(1) Spaceclass Solution: def connect(self, root: 'Node') -> 'Node': if not root: return None level = root while level: node = level lower_node = level = None while node: if node.left: if not level: level = node.left if lower_node: lower_node.next = node.left lower_node = node.left if node.right: if not level: level = node.right if lower_node: lower_node.next = node.right lower_node = node.right node = node.next return rootProblem Explanation
In the first variation of this question, we had a perfect tree, meaning we always had a left child node to build a next pointer bridge from.
In this variation, our tree is a little funky with some of the nodes having children while others don't.
This means that we can't just do a modified Breadth-First Search by continuously stepping down to the left child. Instead, we may need to start a level traversal from a right child of the last node of a level, or some weird scenario similar to that.
This doesn't change the problem logic that much. We will still have one pointer that throws bridges horizontally through the lower level. However, now we will need an additional pointer that throws bridges somewhat vertically to the leftmost node of the lower level so that we know how to get to the next level after we have processed each node within a current level.
First off, if we have no root then we have no next node to connect.
If that is the case, we will return nothing.
if not root: return None
Otherwise, we will initialize our level pointer at the root. This is the pointer that will let us know which bridge we should cross when moving down levels. In this case, we need to throw a bridge to the first level.
level = root
While we still have a node to step down to, we will continue moving down levels.
while level:
At the beginning of each iteration, we will begin our level traversal by crossing the bridge previously set by our level pointer. This pointer will always be at the leftmost position of the tree.
node = level
After we have crossed our bridge down a level, we will clear both our level and lower node pointer so that we can begin creating new bridges to anticipate the journey down to the next level below the current one. This lower node pointer will be the one to create bridges horizontally that we will use to step through each node when we get to the next level.
lower_node = level = None
While our node hasn't reached a null value, we still have nodes we need to travel to within the current level.
while level:
Now we play a game of throwing bridges.
If the current node has a left child, and we have not set the bridge to get down to the next level, we will do that now. Remember, this pointer will indicate the leftmost position of the lower level.
if node.left: if not level: level = node.left
If we have already set a lower node, then that means we have set it somewhere to the left within this lower level. If that is the case, then we can connect that node to the current node's left child to make a horizontal bridge that we'll use to walk to the right within the next iteration.
if lower_node: lower_node.next = node.left
If not, then we can't connect a horizontal bridge at this moment but we will set the lower node pointer to the current node's left child, and hopefully, we will use it to connect a bridge somewhere to the right later.
lower_node = node.left
If the current node has a right child, and we have not set the bridge to get down to the next level, that means that this right child is the leftmost position of the lower level and we will throw a bridge down to it.
if node.right: if not level: level = node.right
If we have already set a lower node, then that means we have set it somewhere to the left within this lower level. If that is the case, then we can connect that node to the current node's right child to make a horizontal bridge that we'll use to walk to the right within the next iteration.
if lower_node: lower_node.next = node.right
If not, then we can't connect a horizontal bridge at this moment but we will set the lower node pointer to the current node's right child, and hopefully, we will use it to connect a bridge somewhere to the right later.
lower_node = node.right
After we have finished setting possible bridges down to and across the current node's children, we will cross the horizontal bridge to the next node.
node = node.next
Once we have broken from the loop, it means we had no lower levels to throw our vertical bridge to, so we will return the root. Now our tree will look like a ladder of linked lists.
return root