Construct Binary Tree from Preorder and Inorder Traversal
Patrick LeatonProblem Description
Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.
Example 1:
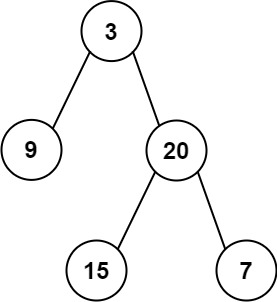
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7]
Example 2:
Input: preorder = [-1], inorder = [-1] Output: [-1]
Constraints:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorderandinorderconsist of unique values.- Each value of
inorderalso appears inpreorder. preorderis guaranteed to be the preorder traversal of the tree.inorderis guaranteed to be the inorder traversal of the tree.
The description was taken from https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/.
Problem Solution
#Recursive DFS# O(N) Time, O(N) Spaceclass Solution: def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode: index = {} for i, value in enumerate(inorder): index[value] = i preorder = preorder[::-1] def dfs(left:int, right:int) -> TreeNode: if left > right: return None root = TreeNode(preorder.pop()) split = index[root.val] root.left = dfs(left, split-1) root.right = dfs(split+1, right) return root return dfs(0, len(inorder)-1)#Iterative DFS#O(N) Time, O(N) Spaceclass Solution: def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode: index = {} for i, value in enumerate(inorder): index[value] = i preorder = preorder[::-1] def dfs() -> TreeNode: stack = [] root = TreeNode(preorder.pop()) stack.append(root) while preorder: child = TreeNode(preorder.pop()) parent = stack[-1] if index[child.val] < index[parent.val]: parent.left = child else: while stack and index[stack[-1].val] < index[child.val]: parent = stack.pop() parent.right = child stack.append(child) return root return dfs()Problem Explanation
Recursive DFS
We are given the preorder traversal and the inorder traversal.
The inorder traversal goes left, root, then right.
The preorder traversal goes root, left, then right.
That means that at the end of the reversed preorder traversal array, we will have the root of each subtree. We can then plug that root into the inorder traversal array to get the left and right children from the left and right indices to any given root index.
That is exactly what we are going to do.
We will start by initializing our index hashmap, then we will go through the inorder traversal array to track the index of each value.
index = {} for i, value in enumerate(inorder): index[value] = i
Afterward, we will reverse the preorder traversal array so that the subtree roots come last instead of first, it will be easy to pop them off this way.
preorder = preorder[::-1]
Next, we will create our recursive dfs function.
The function will take a left and right index of which we will create the bounds of a subarray from the inorder traversal array, which we can then use to create a subtree recursively. Remember, we are taking a root node from the preorder traversal and then splitting a subarray based on that root's index in order to create the subtree.
def dfs(left:int, right:int) -> TreeNode:
Our base case of the function will be that if the left index is greater than the right, then there isn't a subarray we can make subtrees from within this DFS path. If that is the case, we will return from this path.
if left > right: return None
Next, we will pop a subtree root value from the preorder traversal array and create a split variable based on the index of that root within the inorder traversal array.
root = TreeNode(preorder.pop()) split = index[root.val]
After that, we will perform a DFS on the left child, then the right child to create these child subtree nodes.
root.left = dfs(left, split-1) root.right = dfs(split+1, right)
After the DFS yoyo has returned to the current function call, we will return the current subtree root.
return root
Notice in the preorder traversal array and the picture from example one, every left subtree root is traversed before the right.
That is the reason our DFS will have to travel all the way down the left side before moving to the right. Being recursion, we would expect to build the tree from the top to bottom, but since we have our return statement last, we are actually building the tree from the bottom up.
Now that our DFS function is built, all we need to do is make the initial call by passing in the first and last index of the inorder traversal array.
return dfs(0, len(inorder)-1)
Iterative Depth-First Search
The iterative version of this problem is much trickier.
Instead of picking each root recursively for each subtree, we will now be popping each child from the inorder array and attaching the child to the parent which will be in the stack.
Here, we will actually need to compare the index of each child node with its parent node. If the index value of the child is less, then it is a left child. If it is greater, then it is the right child. This is because the inorder traversal goes left, root, right.
We will start by initializing our index hashmap, then we will go through the inorder traversal array to track the index of each value.
index = {} for i, value in enumerate(inorder): index[value] = i
Afterward, we will reverse the preorder traversal array so that the subtree roots come last instead of first, it will be easy to pop them off this way.
preorder = preorder[::-1]
Next, we will create our iterative dfs function.
def dfs() -> TreeNode:
We'll start our function off by initializing a stack, popping the root node off of the preorder traversal array, then pushing that root onto the stack.
stack = [] root = TreeNode(preorder.pop()) stack.append(root)
Then, we will begin our iterations that will continue while the preorder traversal array still has subtree roots that we need to append to our tree.
while preorder:
During each iteration, we can peak at the top of the stack to see what the current parent subtree root is.
Then, we can get the current child subtree root by popping it off of the preorder traversal array.
child = TreeNode(preorder.pop()) parent = stack[-1]
If the index of the child is less than the index of the parent, then the child is the left child.
if index[child.val] < index[parent.val]: parent.left = child
Otherwise, it is the right child and perhaps not of this current parent.
In order to attach the right child, we will need to get the appropriate parent.
The reasoning for this is we are still building the tree from the left subtree roots first, just like in the recursive version because a preorder traversal goes left, right, then root. In the stack, we pushed in the root first and then any left children. If the deepest left subtree had no right children, we would need to pop it off the stack and test the second deepest left subtree as the current parent, and so on.
This solution will be building a tree from the top-down instead of the bottom-up as we did with the recursive version.
In order to do this, we will need to find the first node from the stack that has an index value that is less than the child's index value, as that would be the node that comes directly before the right child within the inorder traversal array since that traversal goes left, root, then right. The first node that satisfies this condition will be its parent node.
else: while stack and index[stack[-1].val] < index[child.val]: parent = stack.pop()
Once the node at the top of the stack has an index value that is greater than the child's, it can no longer be the parent of this child because the right nodes come after the root nodes inside the inorder traversal array. In this case, the last parent we popped off our stack is the parent of this child so we will attach it as the parent's right child, then push the child onto the stack.
parent.right = child stack.append(child)
Once we are out of subtree roots to pop off the preorder stack, our tree is constructed so we will return the root of it.
return root
Now that our DFS function is built, we just need to make the initial call.
return dfs()