Construct Binary Tree from Inorder and Postorder Traversal
Patrick LeatonProblem Description
Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree.
Example 1:
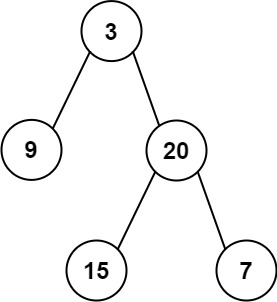
Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] Output: [3,9,20,null,null,15,7]
Example 2:
Input: inorder = [-1], postorder = [-1] Output: [-1]
Constraints:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorderandpostorderconsist of unique values.- Each value of
postorderalso appears ininorder. inorderis guaranteed to be the inorder traversal of the tree.postorderis guaranteed to be the postorder traversal of the tree.
The description was taken from https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/.
Problem Solution
#Recursive DFS#O(N) Time, O(N) Spaceclass Solution: def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode: index = {} for i, value in enumerate(inorder): index[value] = i def dfs(left:int, right:int) -> TreeNode: if left > right: return None root = TreeNode(postorder.pop()) split = index[root.val] root.right = dfs(split+1, right) root.left = dfs(left, split-1) return root return dfs(0, len(inorder)-1)#Iterative DFS#O(N) Time, O(N) Spaceclass Solution: def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode: index = {} for i, value in enumerate(inorder): index[value] = i def dfs() -> TreeNode: stack = [] root = TreeNode(postorder.pop()) stack.append(root) while postorder: parent = stack[-1] child = TreeNode(postorder.pop()) if index[child.val] > index[parent.val]: parent.right = child else: while stack and index[stack[-1].val] > index[child.val]: parent = stack.pop() parent.left = child stack.append(child) return root return dfs()Problem Explanation
Recursive Depth-First Search
We are given the postorder traversal and the inorder traversal.
The inorder traversal goes left, root, then right.
The postorder traversal goes left, right, then root.
That means that at the end of the postorder traversal array, we will have the root of each subtree. We can then plug that root into the inorder traversal array to get the left and right children from the left and right indices to any given root index.
That is exactly what we are going to do.
We will start by initializing our index hashmap, then we will go through the inorder traversal array to track the index of each value.
index = {} for i, value in enumerate(inorder): index[value] = i
Next, we will create our recursive dfs function.
The function will take a left and right index of which we will create the bounds of a subarray from the inorder traversal array, which we can then use to create a subtree recursively. Remember, we are taking a root node from the postorder traversal and then splitting a subarray based on that root's index in order to create the subtree.
def dfs(left:int, right:int) -> TreeNode:
Our base case of the function will be that if the left index is greater than the right, then there isn't a subarray we can make subtrees from within this DFS path. If that is the case, we will return from this path.
if left > right: return None
Next, we will pop a subtree root value from the postorder traversal array and create a split variable based on the index of that root within the inorder traversal array.
root = TreeNode(postorder.pop()) split = index[root.val]
After that, we will perform a DFS on the right child, then the left child to create these child subtree nodes.
root.right = dfs(split+1, right) root.left = dfs(left, split-1)
After the DFS yoyo has returned to the current function call, we will return the current subtree root.
return root
Notice in the postorder traversal array and the picture from example one, every right subtree root is traversed before the left.
That is the reason our DFS will have to travel all the way down the right side before moving to the left. Being recursion, we would expect to build the tree from the top to bottom, but since we have our return statement last, we are actually building the tree from the bottom up.
Now that our DFS function is built, all we need to do is make the initial call by passing in the first and last index of the inorder traversal array.
return dfs(0, len(inorder)-1)
Iterative Depth-First Search
The iterative version of this problem is much trickier.
Instead of picking each root recursively for each subtree, we will now be popping each child from the postorder array and attaching the child to the parent which will be in the stack.
Here, we will actually need to compare the index of each child node with its parent node. If the index value is less, then it is a left child. If it is greater, then it is the right child. This is because the inorder traversal goes left, root, right.
We will start by initializing our index hashmap, then we will go through the inorder traversal array to track the index of each value.
index = {} for i, value in enumerate(inorder): index[value] = i
Next, we will create our iterative dfs function.
def dfs() -> TreeNode:
We'll start our function off by initializing a stack, popping the root node off of the postorder traversal array, then pushing that root onto the stack.
stack = [] root = TreeNode(postorder.pop()) stack.append(root)
Then, we will begin our iterations that will continue while the postorder traversal array still has subtree roots that we need to append to our tree.
while postorder:
During each iteration, we can peak at the top of the stack to see what the current parent subtree root is.
Then, we can get the current child subtree root by popping it off of the postorder traversal array.
parent = stack[-1] child = TreeNode(postorder.pop())
If the index of the child is greater than the index of the parent, then the child is the right child.
if index[child.val] > index[parent.val]: parent.right = child
Otherwise, it is a left child and perhaps not of this current parent.
In order to attach the left child, we will need to get the appropriate parent.
The reasoning for this is we are still building the tree with the right subtree roots first, just like in the recursive version because a postorder traversal goes left, right, then root. From the root, it would be root, right, then left. In the stack, we pushed in the root first and then any right children. If the deepest right subtree had no left children, we would need to pop it off the stack and check the second deepest right subtree, and so on.
This solution will be building a tree from the top-down instead of the bottom-up as we did with the recursive version.
In order to do this, we will need to find the first node from the stack that has an index value greater than the child's index value, as that would be the node that comes directly after the left child within the inorder traversal array since that traversal goes left, root, then right.
else: while stack and index[stack[-1].val] > index[child.val]: parent = stack.pop()
Once the node at the top of the stack has an index value that is less than the child's index value, it can no longer be the parent of this child because it has a lesser index within the inorder traversal array. In this case, the last parent we popped off our stack is the parent of this child, so we will attach it as the parent's left child, then push the child onto the stack so that we can attach any children for it within the next iteration.
parent.left = child stack.append(child)
Once we are out of subtree roots to pop off the postorder stack, our tree is constructed so we will return the root of it.
return root
Now that our DFS function is built, we just need to make the initial call.
return dfs()