Interval List Intersections

Patrick Leaton
Published: May 31, 2021, 4:10 p.m.
Problem Description

You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [starti, endi] and secondList[j] = [startj, endj]. Each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

A closed interval [a, b] (with a < b) denotes the set of real numbers x with a <= x <= b.

The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].

 

Example 1:

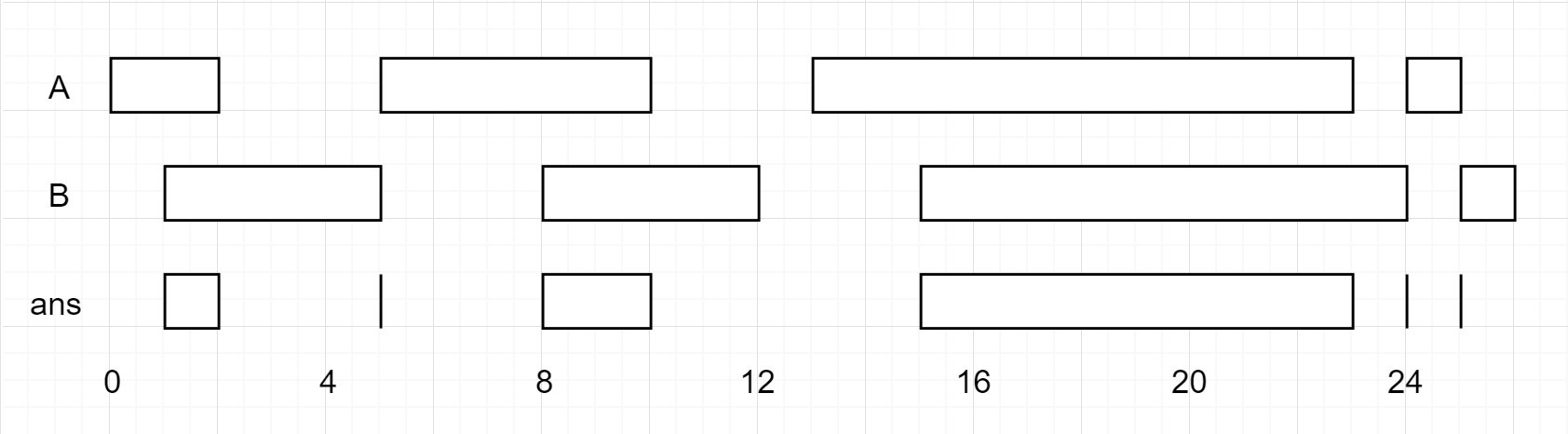
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Example 2:

Input: firstList = [[1,3],[5,9]], secondList = []
Output: []

Example 3:

Input: firstList = [], secondList = [[4,8],[10,12]]
Output: []

Example 4:

Input: firstList = [[1,7]], secondList = [[3,10]]
Output: [[3,7]]

 

Constraints:

  • 0 <= firstList.length, secondList.length <= 1000
  • firstList.length + secondList.length >= 1
  • 0 <= starti < endi <= 10^9
  • endi < starti+1
  • 0 <= startj < endj <= 10^9
  • endj < startj+1

 

The description was taken from https://leetcode.com/problems/interval-list-intersections/.

Problem Solution

#O(M+N) Time, O(1) ADDITIONAL Space
class Solution:
    def intervalIntersection(self, firstList: List[List[int]], secondList: List[List[int]]) -> List[List[int]]:
        output = []
        i, j = 0, 0
        n, m = len(firstList), len(secondList)
       
        def intersect(interval_one:int, interval_two:int) -> list:
            overlap_start = max(firstList[i][0], secondList[j][0])
            overlap_end = min(firstList[i][1], secondList[j][1])
            if overlap_start <= overlap_end:
                output.append([overlap_start, overlap_end])
       
        while i < n and j < m:
            intersect(firstList[i], secondList[j])
            if firstList[i][1] <= secondList[j][1]:
                i += 1
            else:
                j += 1
 
        return output

Problem Explanation

The problem only wants us to see where there are overlaps.  

We aren't being asked to calculate the minimum number of overlaps there could possibly be by removing intervals or something like that which are typical in interval questions that utilize greedy algorithms.

Instead, we can just step through both lists using two pointers to see if there are any overlaps within each iteration's current two intervals.  Since the interval arrays are already sorted, that saves us the hassle of doing it ourselves so we can get a nice linear time complexity.  

We'll start by initializing our output array, our pointers, and the lengths of both lists so we don't have to count that within each iteration.

        output = []
        i, j = 0, 0
        n, m = len(firstList), len(secondList)

Let's now build a helper function to calculate the span of the overlap between two given intervals, if it exists.

        def intersect(interval_one:int, interval_two:int) -> list:

 

Let's go ahead and draw out what this function is going to do, this is a must with interval questions.

We have the test case of having these two interval arrays, [[0,2],[5,10],[13,23]] and [[1,5],[8,12],[15,24]]. 

Let's look at the first two overlapping intervals, [0,2] and [1,5].

We want to first see where the possible overlap would start by getting the greater start time.  We are looking for an overlap where the start time of one interval begins before the previous interval ends, so we will get that greater start time.

             overlap_start = max(firstList[i][0], secondList[j][0])

          
                    
<0-1-2-3-4-5>
 

Next, we will see where the possible overlap would end by getting the lesser end time.  Similarly, we are looking for an overlap where the end time of one interval would come after a second interval starts, so we will get that lesser end time.

          
                    
<0-1-2-3-4-5>
 

Now, if the greatest start time is less than the smallest end time, we have the range of an overlap and we will append that to the output.

          
                    
          
<0-1-2-3-4-5>
 
            if overlap_start <= overlap_end:
                output.append([overlap_start, overlap_end])

In our intervalIntersection function, we will create a loop that will run while both interval array pointers haven't reached the end of their array.

        while i < n and j < m:

 

During each iteration, we will pass the two given intervals that our pointers are on into the intersect function and check for overlaps.

            intersect(firstList[i], secondList[j])

 

If the first list's interval's end-time is less than or equal to the end-time of the interval in the second list, we will move the first list's pointer forward within its array.  If an interval from the second list overlapped with an interval from the first, we want to continue traversing the first list to see if the second list's interval will overlap with any other intervals from the first.

            if firstList[i][1] <= secondList[j][1]:
                i += 1

 

Similarly, if the interval from the first list overlapped with an interval from the second, we want to continue traversing the second list to see if the first list's interval will overlap with any other intervals from the second.  

            else:
                j += 1

 

Once one of the pointers has reached the end of its interval array, we will be done with our traversal so we can return all of the overlap intervals.

        return output