Problem Description
Given the root of a binary tree, return the maximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes are also counted into the length calculation.
It is guaranteed that the answer will in the range of 32-bit signed integer.
Example 1:
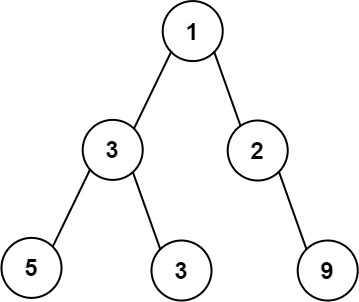
Input: root = [1,3,2,5,3,null,9] Output: 4 Explanation: The maximum width existing in the third level with the length 4 (5,3,null,9).
Example 2:
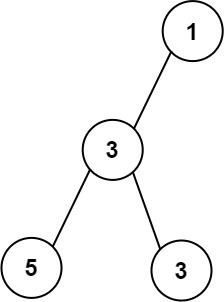
Input: root = [1,3,null,5,3] Output: 2 Explanation: The maximum width existing in the third level with the length 2 (5,3).
Example 3:
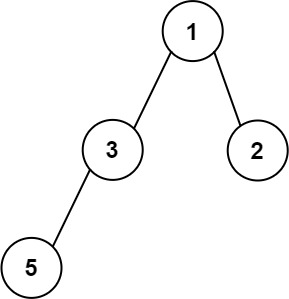
Input: root = [1,3,2,5] Output: 2 Explanation: The maximum width existing in the second level with the length 2 (3,2).
Example 4:
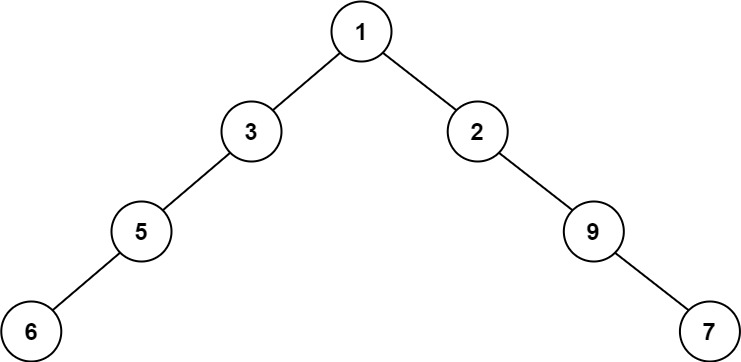
Input: root = [1,3,2,5,null,null,9,6,null,null,7] Output: 8 Explanation: The maximum width existing in the fourth level with the length 8 (6,null,null,null,null,null,null,7).
Constraints:
- The number of nodes in the tree is in the range
[1, 3000]. -100 <= Node.val <= 100
The description was taken from https://leetcode.com/problems/maximum-width-of-binary-tree/.
Problem Solution
#O(N) Time, O(N) Spaceclass Solution: def widthOfBinaryTree(self, root: TreeNode) -> int: def bfs(root:TreeNode) -> int: max_width = 0 queue = collections.deque([(root, 1)]) while queue: layer = len(queue) _, left = queue[0] _, right = queue[-1] max_width = max(max_width, right - left + 1) for _ in range(layer): node, index = queue.popleft() if node.left: queue.append((node.left, 2 * index)) if node.right: queue.append((node.right, 2 * index + 1)) return max_width return bfs(root)Problem Explanation
Since we know we're dealing with the width of a binary tree, that is a good hint that a Breadth-First Search is a good approach to use so that we can search the tree level by level.
However, there is a trick to this problem. In order to not have to append null values, we can calculate the index of each child node by multiplying the current index by two for a left child node, or the current index by two, plus one, for a right child node. This way, we only have non-null values in our queue.
Let's start by creating our bfs function that will take a root node to begin the search.
def bfs(root:TreeNode) -> int:
In our function, we will initialize a width counter and a queue, with the initial index of the root.
max_width = 0 queue = collections.deque([(root, 1)])
Next, we will make a loop that we will use to traverse each layer of the tree that will run until there are no more layers of nodes to process.
while queue:
At the beginning of each iteration, before processing any nodes, we will get a quick count of how many nodes are in the layer to know the number of nodes we need to visit.
layer = len(queue)
Since we aren't adding any null values to our queue, we can't use this value to calculate the width. To do that, we will peek at the index of the most-left node in our queue, subtract that by the index of the most-right node in our queue, then add one.
_, left = queue[0] _, right = queue[-1] max_width = max(max_width, right - left + 1)
We are calculating the width, not the distance, so that is why we add one in the calculation.
If we had this tree below, the width of the second layer would be two. If we just calculated the distance, we would get one, so we need to add two to get the width.
After getting the width of the current layer, we will go through the layer and pop off each node from the queue along with their index values.
for _ in range(layer): node, index = queue.popleft()
If the node we just popped off has a left node, we will push it into the queue with the index value of the current node's index multiplied by two.
if node.left: queue.append((node.left, 2 * index))
If the node we just popped off has a right node, we will push it into the queue with the index value of the current node's index multiplied by two, plus one.
if node.right: queue.append((node.right, 2 * index + 1))
Going back to the example of this small tree below, the root would be index one.
We can calculate that the left child would be index two because two multiplied by one is two.
We can calculate that the right child would be index three because two multiplied by one, plus one, is three.
After we have broken from the loop because there are were more layers to process, we will return the maximum width that we calculated.
return max_width
With the bfs function built, all there is to do now is to make the initial function call from the root.
return bfs(root)