Problem Description
A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).
Return a list of all MHTs' root labels. You can return the answer in any order.
The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
Example 1:
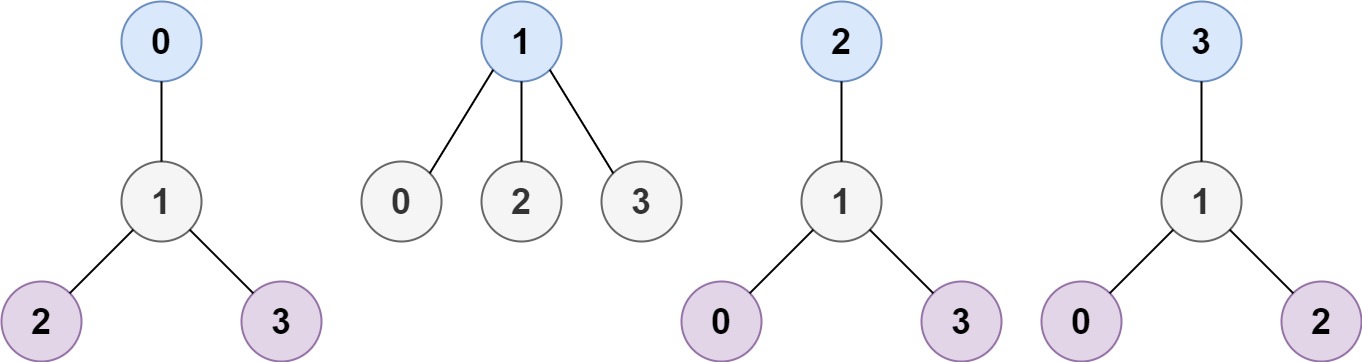
Input: n = 4, edges = [[1,0],[1,2],[1,3]] Output: [1] Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.
Example 2:
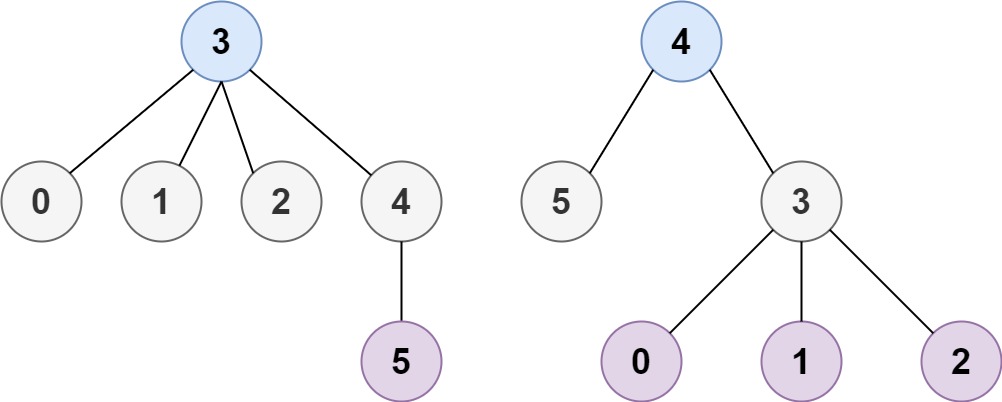
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]] Output: [3,4]
Example 3:
Input: n = 1, edges = [] Output: [0]
Example 4:
Input: n = 2, edges = [[0,1]] Output: [0,1]
Constraints:
1 <= n <= 2 * 10^4edges.length == n - 10 <= ai, bi < nai != bi- All the pairs
(ai, bi)are distinct. - The given input is guaranteed to be a tree and there will be no repeated edges.
The description was taken from https://leetcode.com/problems/minimum-height-trees/.
Problem Solution
#O(N) Time, O(N) Space
class Solution:
def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
if n <= 2:
return range(n)
adjacency = {}
queue = collections.deque()
for node in range(0, n):
adjacency[node] = []
for node, neighbor in edges:
adjacency[node].append(neighbor)
adjacency[neighbor].append(node)
for node in range(0, n):
if len(adjacency[node]) == 1:
queue.append(node)
while n > 2:
width = len(queue)
n -= width
for _ in range(width):
node = queue.popleft()
for neighbor in adjacency[node]:
adjacency[neighbor].remove(node)
if len(adjacency[neighbor]) == 1:
queue.append(neighbor)
return queue
Problem Explanation
If we view a tree as a spiderweb of nodes, we can find the root node which would be the center of the web, by continuously removing the outer layer of the web.
This can be achieved through a Breadth-First Search level-order traversal where we visit the outer layer within each iteration.
Within our search, we will continually trim each layer of leaf nodes off until there are either one or two nodes remaining, which we will choose are our root(s). This algorithm is also known as Topological Sorting.
Only being able to have one or two roots is similar to how a palindrome only has a center of one or two elements. If there were three elements, then the center would just be the middle element. Here, we could be left with either two nodes that are connected to each other or just one node, because if we had three, the center would just be the middle node.
First off, if our input is less than equal to two elements, then we can just choose these as the root(s) of the tree. If it were one, we'd have one root. If it were two, we would have two roots connected to each other.
if n <= 2: return range(n)
Otherwise, we will start by initializing our adjacency list that maps each neighbor to each node so that we can graph a tree without physically instantiating nodes using the edges input.
adjacency = {}
Once we have initialized the adjacency list, we will go through each node and place it in the adjacency list with an, initially, empty list of neighbors.
for node in range(0, n): adjacency[node] = []
Since this is an undirected graph, the edge between each node and each neighbor goes to and from each other.
To signify this, we will go through the edges input and map each node to its neighbor, then each neighbor to the node, so that it is a two-way edge, undirected edge.
for node, neighbor in edges: adjacency[node].append(neighbor) adjacency[neighbor].append(node)
Next, we will traverse each node in the adjacency list, and if any node only has one neighbor, then that node is a leaf so we will add it to the first layer of nodes to be visited within our search.
for node in range(0, n):
if len(adjacency[node]) == 1:
queue.append(node)
While we have more than two leaves, we don't have our root(s) yet, so we will need to continue trimming leaves.
while n > 2:
Before trimming the current layer of leaves, we will first get the width of our queue.
This will let us know how many leaf nodes are within the current layer we are about to visit, and we will then subtract that layer count by our total count of nodes remaining within our search.
width = len(queue)
n -= width
Then, for each node within the current layer, we will pop the node from our queue.
for _ in range(width):
node = queue.popleft()
We will then remove that node from its neighbors' adjacency lists, essentially removing it from our tree graph.
for neighbor in adjacency[node]:
adjacency[neighbor].remove(node)
If we find that our neighbor is now a leaf node, meaning that it has one node within its adjacency list which would be its parent node, we will add it to the queue and we will visit it to trim it within the next layer.
if len(adjacency[neighbor]) == 1:
queue.append(neighbor)
Once we have broken from our loop, we have one or two nodes left in our queue.
These will be our root(s).
return queue