Problem Description
Given the root of a binary tree and an integer targetSum, return all root-to-leaf paths where each path's sum equals targetSum.
A leaf is a node with no children.
Example 1:
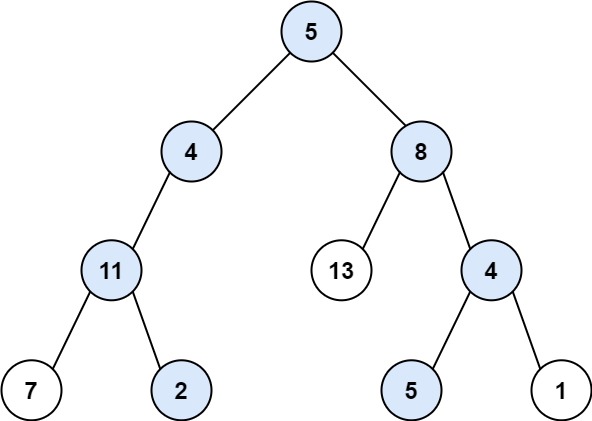
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 Output: [[5,4,11,2],[5,8,4,5]]
Example 2:
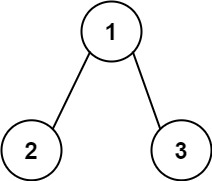
Input: root = [1,2,3], targetSum = 5 Output: []
Example 3:
Input: root = [1,2], targetSum = 0 Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 5000]. -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
The description was taken from https://leetcode.com/problems/path-sum-ii/.
Problem Solution
#O(N) Time, O(N) Spaceclass Solution: def pathSum(self, root: TreeNode, targetSum: int) -> List[List[int]]: output = [] def backtrack(node: TreeNode, combo:list, curr_sum:int) -> None: if not node: return combo.append(node.val) curr_sum += node.val if curr_sum == targetSum and not node.left and not node.right: output.append(list(combo)) backtrack(node.left, combo, curr_sum) backtrack(node.right, combo, curr_sum) curr_sum -= node.val combo.pop() backtrack(root, [], 0) return outputProblem Explanation
The solution is very similar to the problem Target Sum.
We are given an input of values and asked to return all path combinations where the values sum to the target.
When we see an exhaustive requirement like this, we can consider using backtracking to generate every possible combination then return the ones that fit the constraint, in this case, the ones that sum to the given target.
Let's start by initializing our output array.
output = []
Then, we can build our recursive, backtrack function.
Each function call will take a current node, a current combo that indicates which path the Depth-First Search took, and a current sum of the nodes within the given path.
def backtrack(node: TreeNode, combo:list, curr_sum:int) -> None:
If our DFS has reached a null node, we will return from the path.
if not node: return
Otherwise, we will add the current node value to the current combo and the current sum.
combo.append(node.val) curr_sum += node.val
The problem requires us to return only the root-to-leaf combo where the sum of the elements equals the target, so we will know if we have satisfied that constraint if the current sum reaches a node that has no children.
If that is the case, we will append the current DFS path combination to the output, converting it to a list prior so that we save a deep copy instead of a shallow copy of reference pointers that would be overwritten later from the recursive calls.
if curr_sum == targetSum and not node.left and not node.right: output.append(list(combo))
After that, we will continue our DFS on the left and right children while remembering to pass the combo and the sum of the current path, so that we can continue getting every possible path combination and sum.
backtrack(node.left, combo, curr_sum) backtrack(node.right, combo, curr_sum)
Once the DFS has returned to the current function call, we will remove the node value from the current sum and the current combo.
This will allow us to swap out node values for other node values to continue getting each root-to-leaf combination.
curr_sum -= node.val combo.pop()
Now that our function is built, we just need to make the initial call with the current node being the root, the current combo being empty, and the current sum being zero.
Once the backtracking has been completed, we will have every root-to-leaf combination that sums to the target value.
backtrack(root, [], 0) return output