Problem Description
Given the root of a binary tree, return the zigzag level order traversal of its nodes' values. (i.e., from left to right, then right to left for the next level and alternate between).
Example 1:
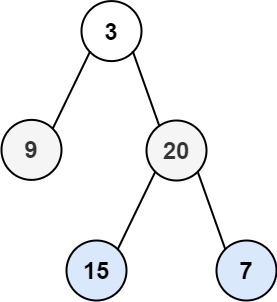
Input: root = [3,9,20,null,null,15,7] Output: [[3],[20,9],[15,7]]
Example 2:
Input: root = [1] Output: [[1]]
Example 3:
Input: root = [] Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 2000]. -100 <= Node.val <= 100
The description was taken from https://leetcode.com/problems/binary-tree-zigzag-level-order-traversal/.
Problem Solution
#O(N) Time, O(N) Spaceclass Solution: def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]: if not root: return root level_order = [] def bfs(root: TreeNode) -> None: queue = collections.deque([root]) level = 0 while queue: level_order.append([]) level_width = len(queue) for _ in range(level_width): node = queue.popleft() level_order[level].append(node.val) if node.left: queue.append(node.left) if node.right: queue.append(node.right) if level%2 == 1: level_order[level] = level_order[level][::-1] level += 1 bfs(root) return level_orderProblem Explanation
If the problem gives us a graph and tells us to traverse it level by level or layer by layer, that is typically an indication that a Breadth-First Search can be used.
This is just an ordinary level order traversal, the only thing we need to add is a check to see if the current level is even or odd. If it is odd, we will reverse the level in the output array.
First off, if there is no root that was input, we have nothing to traverse so we are done.
return root
Otherwise, we will start by initializing our output array.
level_order = []
Next, we will create our bfs function.
def bfs(root: TreeNode) -> None:
We'll initialize a queue from a deque and push the root into it.
Next, we will keep a level counter to keep track of which row we are currently appending the current level to within the output array.
queue = collections.deque([root]) level = 0
Then, we will create a loop that will run while the queue still has nodes we need to process.
while queue:
Before processing any nodes, we will first append an empty row to the output array and count the nodes that are currently in the queue so that we know how long our iteration should be.
level_order.append([]) level_width = len(queue)
Now we can start writing the main BFS logic.
For each node in the current level, we will pop the node off of the queue, append its value to the current level of the output array and then push all of its children into the queue.
for _ in range(level_width): node = queue.popleft() level_order[level].append(node.val) if node.left: queue.append(node.left) if node.right: queue.append(node.right)
Once all of the nodes have been processed and appended for the current level, we will check if the current level is odd by utilizing the modulus operator.
If the level modded by two has one leftover, then it is odd and we will reverse the current level.
Otherwise, this will be skipped.
if level%2 == 1: level_order[level] = level_order[level][::-1]
We can then increment the level counter and prepare to process the next level.
level += 1
Now, all we need to do is make the initial function call by passing the root.
Once the BFS is complete, we will return the level_order output array.
bfs(root) return level_order