Problem Description
Given the root of a binary search tree, and an integer k, return the kth (1-indexed) smallest element in the tree.
Example 1:
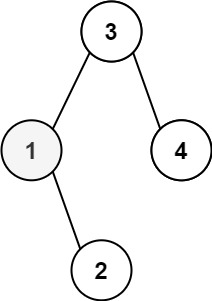
Input: root = [3,1,4,null,2], k = 1 Output: 1
Example 2:
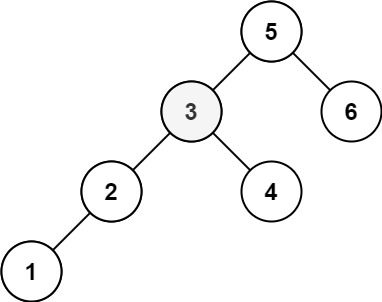
Input: root = [5,3,6,2,4,null,null,1], k = 3 Output: 3
Constraints:
- The number of nodes in the tree is
n. 1 <= k <= n <= 10^40 <= Node.val <= 10^4
Follow up: If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?
The description was taken from https://leetcode.com/problems/kth-smallest-element-in-a-bst/.
Problem Solution
#Recursive Inorder DFS#O(N) Time, O(N) Spaceclass Solution: def kthSmallest(self, root: TreeNode, k: int) -> int: if not root: return tree_values = [None] def inorder(node: TreeNode) -> None: if not node: return inorder(node.left) tree_values.append(node.val) inorder(node.right) inorder(root) return tree_values[k]#Iterative DFS#O(N) Time, O(N) Spaceclass Solution: def kthSmallest(self, root: TreeNode, k: int) -> int: if not root: return stack = [] kth_smallest, node = None, root self.stack_left_children(node, stack) while kth_smallest is None: node = stack.pop() k -= 1 if not k: kth_smallest = node.val self.stack_left_children(node.right, stack) return kth_smallest def stack_left_children(self, node: TreeNode, stack) -> list: while node: stack.append(node) node = node.left return stack
Problem Explanation
The order of values in a BST, in order range from left, root, right.
If we go to the far-left node of the tree, that will be the smallest value of the tree. Its parent will be the second smallest, and the parent's right child would be the third smallest if it isn't null.
The most straightforward way to get the kth smallest element is to perform an inorder tree traversal as outlined previously, and save each value we come across within an array. Once we have traversed each node, we can return the element in the kth index of the array.
Recursive Solution
First off, if there is not a root, then we don't have a kth smallest element so we will return.
if not root: return
Otherwise, we will create an array that will store the node values in order.
Let's initialize the zeroth index as none since we'll be counting the smallest elements starting from one.
tree_values = [None]
Now we can create our recursive, inorder function.
def inorder(node: TreeNode) -> None:
Since it is a recursive function, let's make sure to set our base case first.
The base case is if the function was called on a null root. If that is the case, we will return.
if not node: return
Otherwise, we will recursively call the function on the left node, we will append the current node, then call the function on the right node.
inorder(node.left) tree_values.append(node.val) inorder(node.right)
Remember, recursion and stacks are both last in, first out.
That means that this function is going to search all the way down the left side of the tree until it hits a null node. When that happens, the last node put into the recursive stack would be the far-left node.
It then returns from the null value, appends its current value to the tree_values array, then it will recurse the right child before the parent node can be popped off the recursive call stack for the same process. This will happen until the far-right node is traversed and we will have every element sorted in order.
After we have called this function on the initial root, we just need to return the kth index.
inorder(root) return tree_values[k]
Iterative Solution
The iterative solution is a little trickier.
This is because we need to manually pop off the left nodes from the stack, decrement k, and fill the stack with the right node's left children.
What we can do is have one function that fills the stack and another function that pops the stack, then calls the other function on the right child.
First off, if there is not a root, then we don't have a kth smallest element so we will return.
if not root: return
Otherwise, we will initialize our stack, our kth_smallest value to none, and our initial node pointer to the root.
stack = [] kth_smallest, node = None, root
Let's now make our stack_left_children function that will start from a given node and put the left branch up until that node onto the stack. This ensures that we are popping off the smallest value from the stack each time.
The function will have a loop that will run until it hits a null value. During each iteration, we will put the current node onto the stack and then iterate to the left child.
def stack_left_children(self, node: TreeNode, stack) -> list: while node: stack.append(node) node = node.left return stackAs mentioned in the recursive solution, we want to utilize the last in, first out property of stacks. The first value we pop off of the stack will be the last one that went in, which will be the far-left node of the stack, then its parent, then the left children of the right node, then the right node until we have gotten the kth smallest node.
Moving back to the other function, we will create a loop that will run until we have found the kth smallest element.
while kth_smallest is None:
During each iteration, we will pop the smallest value off of the stack, decrement k, and if we haven't decremented k to zero then we still need to traverse more nodes so we will fill the stack with the left branch of the right node.
node = stack.pop() k -= 1 if not k: kth_smallest = node.val self.stack_left_children(node.right, stack)
Once we have the kth_smallest value, we will return it.
return kth_smallest