Problem Description
Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.
class Node {
public int val;
public List<Node> neighbors;
}
Test case format:
For simplicity sake, each node's value is the same as the node's index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list.
Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.
Example 1:
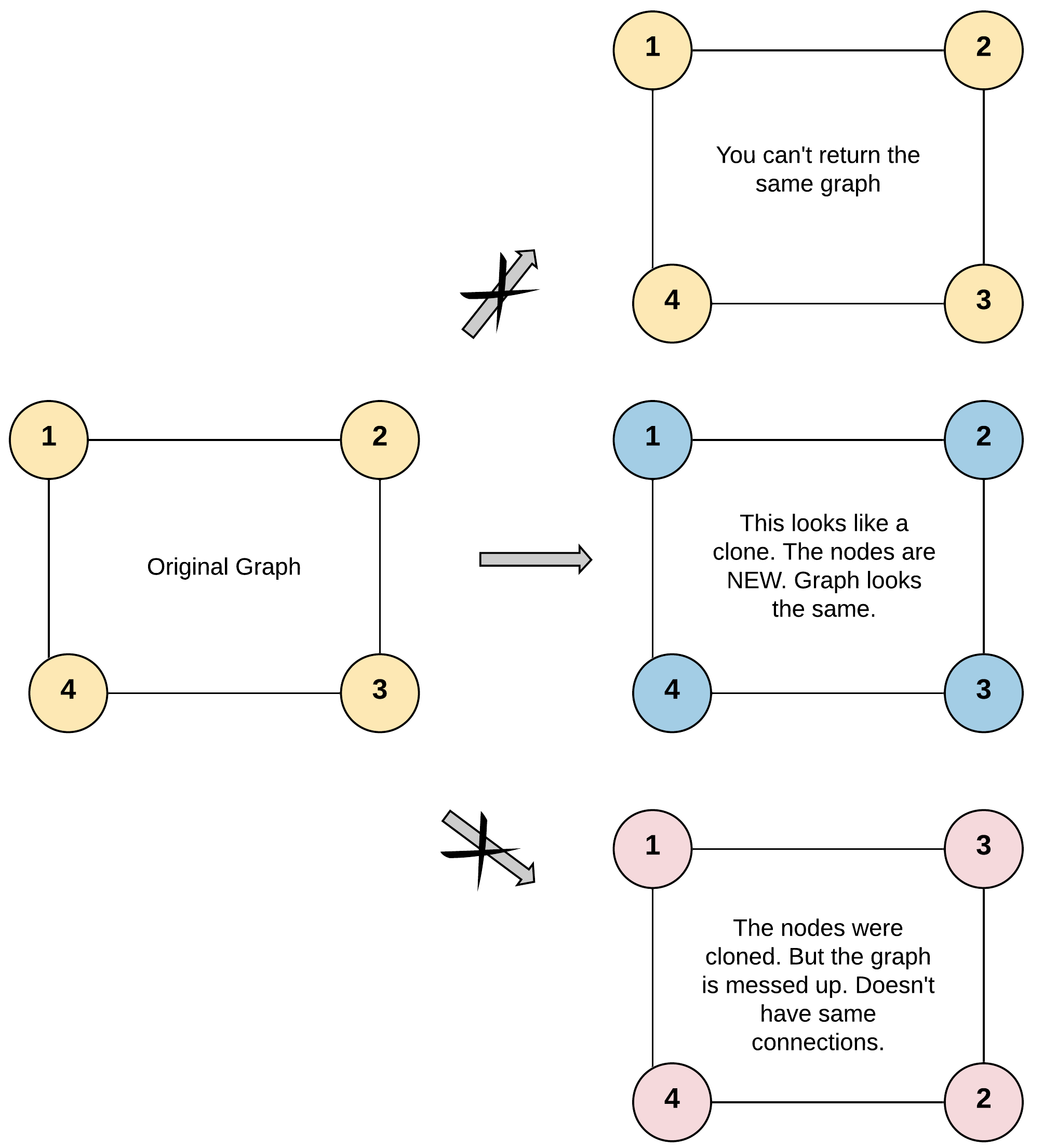
Input: adjList = [[2,4],[1,3],[2,4],[1,3]] Output: [[2,4],[1,3],[2,4],[1,3]] Explanation: There are 4 nodes in the graph. 1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4). 2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3). 3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4). 4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
Example 2:
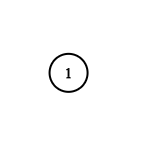
Input: adjList = [[]] Output: [[]] Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
Example 3:
Input: adjList = [] Output: [] Explanation: This an empty graph, it does not have any nodes.
Example 4:
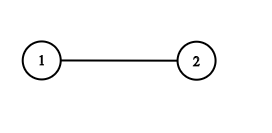
Input: adjList = [[2],[1]] Output: [[2],[1]]
Constraints:
1 <= Node.val <= 100Node.valis unique for each node.- Number of Nodes will not exceed 100.
- There is no repeated edges and no self-loops in the graph.
- The Graph is connected and all nodes can be visited starting from the given node.
The description was taken from https://leetcode.com/problems/clone-graph/.
Problem Solution
#O(M+N) Time, O(N) Spaceclass Solution: def cloneGraph(self, node: 'Node') -> 'Node': if not node: return None seen = {} def dfs(node: 'Node') -> 'Node': node_copy = Node(node.val) seen[node_copy.val] = node_copy neighbor_copies = [] for neighbor in node.neighbors: if neighbor.val not in seen: neighbor_copies.append(dfs(neighbor)) else: neighbor_copies.append(seen[neighbor.val]) node_copy.neighbors = neighbor_copies return node_copy return dfs(node)Problem Explanation
We can solve this problem using Depth First Search.
We will initialize a given node, but we can't make a copy of the node's neighbors until we have initialized those nodes as well.
This is where the DFS will come into play.
We can initialize a node, add it to a Hashmap with the node's value being the dictionary key and the node instance being the dictionary value. This is how we can account for existing nodes and also prevent ourselves from entering graph cycles.
Once each of a given node's neighbors has been instantiated, and their neighbors have been instantiated, we can make a copy of the node's neighbors and successfully copy a node. Once each node has been copied with its val and neighbors attributes, we have copied the graph.
If we received an empty adjacency list then we have no graph, so we don't have to clone anything.
If this happens, we can return none.
if not node: return None
Otherwise, let's start by initializing our seen HashMap to signify the attendance of our nodes.
seen = {}
Now we will create our dfs function, it will accept a node as an argument and will return a node.
def dfs(node: 'Node') -> 'Node':
We'll instantiate a new node using the value of the node we're copying that was just passed to the current DFS function call, recall that this value is taken from the node's index within the adjacency list.
node_copy = Node(node.val)
Then, we will add the node to the seen dictionary, basically saying that this node exists and we have seen it within a recursive call. The node's value will be the dictionary key and the physical node instance will be the dictionary value.
seen[node_copy.val] = node_copy
Now that we have the node's value copied, we also need to copy the list of neighbors that a node object has as an attribute as well.
For this, we need to initialize an empty array and begin seeing where these copies are in our dictionary so that we can finish creating this node.
neighbor_copies = []
The biggest problem we are going to run into when copying these neighbors is we can't make a copy of a node that hasn't been created yet. We can't ask for our Uncle Joe to cosign a lease on an apartment if he was never born. So, before we try to make a copy of a given node's neighbors, we are going to need to make sure they were created.
For each neighbor of the node that we're copying in a given function call, we are going to need to make sure that we have made a copy of them by checking if they are in seen.
If they're not, we need to perform a DFS, passing the neighbor into the function as the node to be copied.
if neighbor.val not in seen: neighbor_copies.append(dfs(neighbor))
If they are in seen, we know they exist and we know where they exist, so we can append their instance to our neighbors array.
else: neighbor_copies.append(seen[neighbor.val])
Once each neighbor has been accounted for, we can finish our node copy by setting its neighbors attribute to the neighbor_copies array and return the node copy.
node_copy.neighbors = neighbor_copies return node_copy
Once the DFS function has been built, all there is to do now is make the initial call.
return dfs(node)
Additional Notes
So what's the point of this, right?
The point of the solution is being aware of the viability of a HashMap within the scope of DFS algorithms. Without the seen dictionary, we wouldn't be aware if we made multiple copies of neighbors for each node, we could have a quadratic lookup time if we tried to lookup neighbors saved to an array or linked list for example, or we also could have ended up in a lookup cycle. If for example, we were trying to create node one that was connected to node two, then we weren't sure if node two existed so we ran a DFS on it, we would end up asking the question in the node two DFS, but for node one, creating a cycle.
We can view this as throwing a party for a few of our friends and calling them to see if they can make it. We would call friend one first and see if he's going, and he/she says, "well, I'll go if friends two and four are going". Then we would call friend two and they would say "well, I'll go if friends one and three are going". Then, we'd call friend one again and they would say the same thing, we wouldn't actually have an answer to who is going to the party so we would have to keep calling friends one and two. The HashMap provides an answer to the question of "which nodes do we have and where are they?".