Problem Description
Given the head of a linked list, rotate the list to the right by k places.
Example 1:
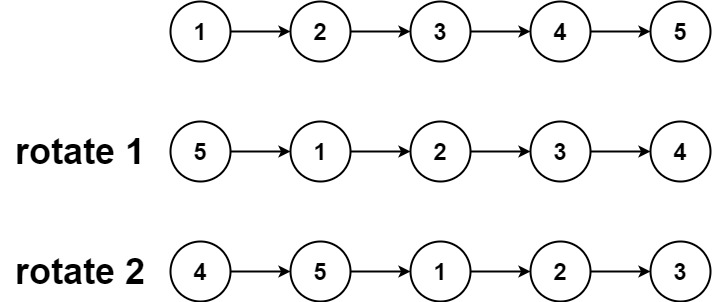
Input: head = [1,2,3,4,5], k = 2
Output: [4,5,1,2,3]
Example 2:
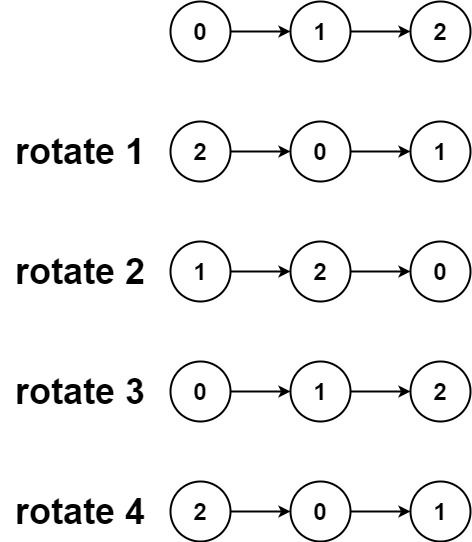
Input: head = [0,1,2], k = 4
Output: [2,0,1]
Constraints:
-
The number of nodes in the list is in the range
[0, 500]. -
-100 <= Node.val <= 100 -
0 <= k <= 2 * 10^9
The description was taken from https://leetcode.com/problems/rotate-list/.
Problem Solution
#O(N) Time, O(1) Spaceclass Solution: def rotateRight(self, head: ListNode, k: int) -> ListNode: if not head or not head.next or k==0: return head ring = head n = 1 while ring.next: ring = ring.next n += 1 k%=n if k == 0: return head ring.next = head tail_place = n - k new_tail = head for i in range(1,tail_place): new_tail = new_tail.next new_head = new_tail.next new_tail.next = None return new_head Problem Explanation
Unlike the problem Rotate Array where if we wanted to take an element off the back of an array and place it on the front we would have to shift each element over one place making the time complexity quadratic, we can take advantage of the linked list data structure.
With the linked list, we don't need to shift any nodes over at all when we remove an element, we just move node pointers. Not only that but with a linked list unlike an array that has a static set of indices mapped to elements, a linked list's order is determined by where the first node begins and the last node ends.
To take advantage of this, we can just make the linked list into a ring and break it between where the new tail and new head will fall, based on the resulting rotation.
First off, if we didn't get a linked list of at least two elements input then we can't rotate the list so we will end here by returning None or the single node we received. Also, if the k value is zero, then we aren't rotating the list so the output list will be the same.
if not head or not head.next or k==0: return head
Let's go ahead and close the linked list off into a ring.
We don't yet know how many nodes we have, and we will need to know that to determine how many places over to move the new head and tail. To figure this out, we will increment a counter each time we iterate to a new node.
We will create a ring pointer and an n counter.
ring = head n = 1
While the next node isn't None, meaning that we haven't reached the tail of the input linked list, we will continue to iterate to the next node and increment the node count.
while ring.next: ring = ring.next n += 1
Once we have traversed the linked list once, we will know how many nodes we have and we can use this value to get rid of any 360-degree rotations since the resulting list will be the same with or without them, but our time complexity can lessen if we avoid them.
For example, if n is five and k is five, we would do a full rotation to get the same list. The same can be said if k is seven and n is five. We would do a full rotation to get the same list, then rotate the array three times when we could have just rotated the array three times.
k%=n
Before we close off the list into a ring, let's add an optimization.
If k is now zero because it was originally a multiple of the node count, we don't need to do any rotations so we can just return the list as is. We'll need to do it before closing it off as it will then be circular and incorrect.
This step isn't required.
if k == 0: return head
We'll finish this portion of the algorithm by closing off the list by pointing the current tail's next pointer away from the None value it is currently pointing at and instead, point it at the current head.
ring.next = head
The new tail place is going to be k places from the end of the list. Let's take this input for example:
Input: [1,2,3,4,5], k=1:
Output: [5,1,2,3,4].
We can see above that the new tail is one to the left of the last node, and the new head is one node after that.
tail_place = n - k
We'll do our final pass over the linked list to set the tail and head positions.
We will set a new_tail pointer at the head, then keep iterating to move it into place. Since we started our n counter from one, it makes sense to start our position counter from one instead of zero as well so that we don't have to break from the loop one count away from the tail_place position.
new_tail = head for i in range(1,tail_place): new_tail = new_tail.next
We will then make the node after the new tail the new head, break the ring into our new linked list and return it.
new_head = new_tail.next new_tail.next = None return new_head