Problem Description
Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.
Notice that you should not modify the linked list.
Example 1:
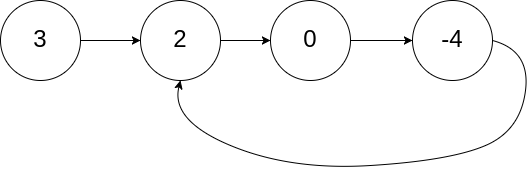
Input: head = [3,2,0,-4], pos = 1 Output: tail connects to node index 1 Explanation: There is a cycle in the linked list, where tail connects to the second node.
Example 2:
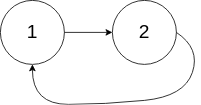
Input: head = [1,2], pos = 0 Output: tail connects to node index 0 Explanation: There is a cycle in the linked list, where tail connects to the first node.
Example 3:

Input: head = [1], pos = -1 Output: no cycle Explanation: There is no cycle in the linked list.
Constraints:
- The number of the nodes in the list is in the range
[0, 104]. -105 <= Node.val <= 105posis-1or a valid index in the linked-list.
Follow up: Can you solve it using O(1) (i.e. constant) memory?
Problem Solution
#O(N) Time, O(1) Spaceclass Solution: def detectCycle(self, head: ListNode) -> ListNode: if head is None: return None def race(head: ListNode) -> ListNode: slow = fast = head while fast and fast.next: slow = slow.next fast = fast.next.next if fast == slow: return fast return None fast = race(head) if fast is None: return None slow = head while slow != fast: slow = slow.next fast = fast.next return slowProblem Explanation
Without using any kind of counter or additional space, we can solve this by using Floyd's Tortoise and Hare algorithm. When we see the word "cycle" for list problems, we should consider using this algorithm.
This is nearly the same solution as the Find the Duplicate Number question, with only slight differences.
We will start by seeing if the linked list we've been given is empty, if that is the case there can't be a cycle.
if head is None: return None
Next, we will create the race function that will check if there is a cycle or not.
We will start by putting our fast and slow pointers at the head of the linked list.
slow = fast = head
We will then make a loop that will run until the fast pointer has either reached the end of the list or has lapped around and met the slow pointer.
while fast and fast.next:
During each iteration, we will increment the slow pointer once and the fast pointer twice.
If the fast pointer has reached the slow pointer, we will return the node the fast pointer is at.
slow = slow.next fast = fast.next.next if fast == slow: return fast
If the fast pointer has reached the end of the list, then that means there is no cycle and we will return none.
return None
Next, we will remake our fast pointer in the outer function. It will be set to the output node of the race function.
We will also check if it is none since that would mean there is no cycle so we would return none.
fast = race(head) if fast is None: return None
After the race, we'll put the slow pointer back at the head of the linked list.
slow = head
We will increment the slow and fast pointer at the same speed until they meet again.
When this happens, they will have met at the entrance to the cycle which is the duplicate number.
while slow != fast: slow = slow.next fast = fast.next
After the two pointers meet, we can return either pointer since they will both be at the start of the cycle.
return slow