Problem Description
Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.
Example 1:
Input: nums = [1,2,3] Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
Example 2:
Input: nums = [0,1] Output: [[0,1],[1,0]]
Example 3:
Input: nums = [1] Output: [[1]]
Constraints:
1 <= nums.length <= 6-10 <= nums[i] <= 10- All the integers of
numsare unique.
The description was taken from https://leetcode.com/problems/permutations/.
Problem Solution
#O(N*N!) Time, O(N*N!) Spaceclass Solution: def permute(self, nums: List[int]) -> List[List[int]]: output = [] def backtrack(start: int) -> None: if start == len(nums): output.append(list(nums)) return for i in range(start, len(nums)): nums[start], nums[i] = nums[i], nums[start] backtrack(start + 1) nums[start], nums[i] = nums[i], nums[start] backtrack(0) return outputProblem Explanation
If a problem requires us to return all possible combinations of a given input, typically that is an indication that backtracking is a good approach.
Backtracking is a Depth-First Search algorithm where we remove a choice whenever the DFS path yoyo returns to the given function. This allows us to circulate elements into each valid position so that we can generate each valid combination.
A general template for backtracking is to set a base case that appends a valid combination for a given DFS path to the output, if not, check if a placement is valid then make the placement. Once that placement is made, we'd go down a new DFS path with that placement and if that path didn't lead to a solution or it didn't lead to every solution like in this problem, we'd backtrack on the choice to make that placement by removing it from the combination.
Let's start by initializing our output array.
output = []
Next, we will initialize our backtrack function.
The function will take a starting index that will be the starting point for a function call's traversal through the input array.
def backtrack(start: int) -> None:
The base case we will want to check at the beginning of each function call is if the starting index has reached the last index of the input array. If that is the case then we will append the current combination of the numbers we have swapped within the input array before returning out of the function. We will need to take a deep copy of the combo since it will be edited later and we don't want it to be overwritten.
if start == len(nums): output.append(list(nums)) return
We will now start creating the backtracking logic.
Let's create a loop that will scan the input array from a given starting index to the last index of the array.
This is how we will split up the scope of each permutation through recursion.
for i in range(start, len(nums)):
Within the current recursive call, we will swap the element in the start index with the element in the current iteration's index.
Afterward, we will recurse the function and increment the starting index by one.
nums[start], nums[i] = nums[i], nums[start] backtrack(start + 1)
Once a Depth First Search path is complete, meaning that we have moved down a recursive path and swapped values until we have met our base case of the starting index reaching the last index of the array, or a called function has iterated all the way to the end of the input array and has broken from the loop, we will then backtrack.
We do this by reverting the swap we implemented previously.
We'll want to do this so that we don't ruin the baseline that a future DFS path will begin on.
For example, if we had [1,2,3] and we just kept swapping values and never backtracked to revert our changes, we are likely going to miss permutations and get duplicate permutations as well.
nums[start], nums[i] = nums[i], nums[start]
Once our backtrack function is created, we will just need to make the initial call by passing zero as the starting index.
Once we have all possible permutations, we will return the output array that contains each permutation.
backtrack(0) return output
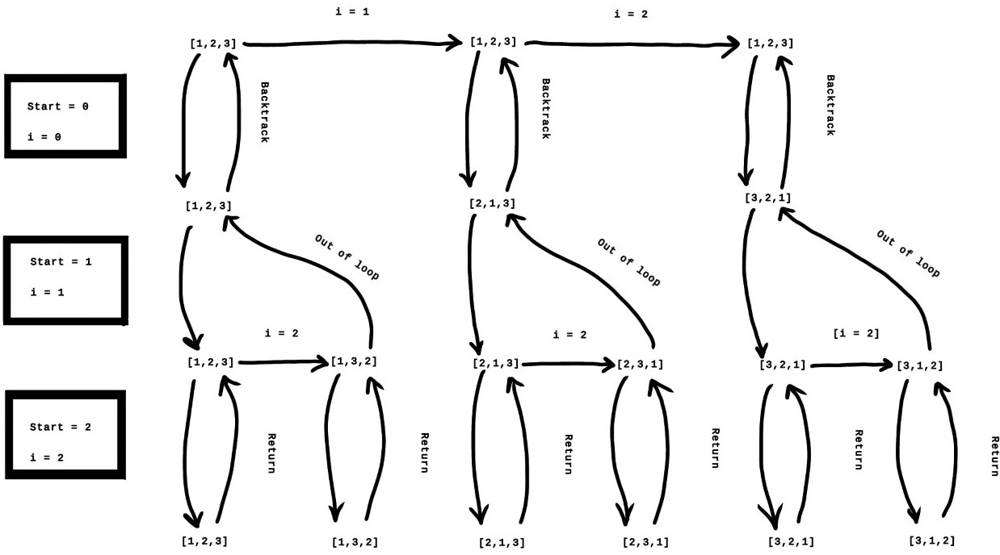
This illustration shows what the flow of the DFS and backtracking would look like for the input [1,2,3].