Problem Description
Given a collection of integers that might contain duplicates, nums, return all possible subsets (the power set).
Note: The solution set must not contain duplicate subsets.
Example:
Input: [1,2,2] Output: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]
The description was taken from https://leetcode.com/problems/subsets-ii/.
Problem Solution
#O(N*2^N) Time, O(N*2^N) Spaceclass Solution: def subsetsWithDup(self, nums: List[int]) -> List[List[int]]: nums = sorted(nums) output = [] def backtrack(start:int, combo:list)-> None: if len(combo) == sub_length: output.append(list(combo)) return for i in range(start, len(nums)): if i > start and nums[i] == nums[i-1]: continue combo.append(nums[i]) backtrack(i+1,combo) combo.pop() for sub_length in range(0, len(nums)+1): backtrack(0, []) return output Problem Explanation
If a problem requires us to return all possible combinations of a given input, typically that is an indication that backtracking is a good approach.
This solution is basically the same as the first Subsets question with the only difference being that we are going to sort the list and skip over any neighboring duplicate values from the input array.
Let's by sorting our input array and initializing our output array.
nums = sorted(nums) output = []
Next, we will create our recursive backtrack function.
The function will take an index to begin a traversal from and a combo list that contains a Depth First Search path's current subset.
def backtrack(start:int, combo:list)-> None:
Before editing a combo any further, we will first check if the length of the combo is equal to the current subset length we are trying to get each combination for.
If it is, we will append the combo to the output and end this recursive path. We will need to take a deep copy of the combo since it will be edited later and we don't want it to be overwritten.
if len(combo) == sub_length: output.append(list(combo)) return
We will now start creating the backtracking logic.
Let's create a loop that will scan the input array from a given starting index to the last index of the array.
This is how we will split up the scope of each subset through recursion.
for i in range(start, len(nums)):
During an iteration, to skip appending duplicate combinations to the output, we will check if we have a previous index within the current recursive tree level by looking at our current i value compared to the starting index. And if we do, that the previous index isn't a duplicate of the current one.
We want to make sure that the first part of that condition is checked because, for example, let's take an input of [1,2,2].
We will have a DFS path that will go from [1], recurse to [1,2], then when it recurses to what should be [1,2,2], it would skip the second two and not ever append [1,2,2] to the output.
We are still wanting duplicate values within the subsets, just not duplicate subsets.
if i > start and nums[i] == nums[i-1]: continue
Within a recursive call, we will append the number at the index of the current iterator value, then recurse the function with the current combo and increment the starting index value to the digit after the current one.
combo.append(nums[i]) backtrack(i+1,combo)
Once a DFS path is complete, we will backtrack by popping the last value off of our combo so that we can append the next number from our input array and begin a new DFS path until we have each subset for a given length.
combo.pop()
Once we have our backtrack function built, we will iterate through the different lengths of subsets and get each unique combination for each length.
In other words, we are getting each combination for subsets of length zero, length one, length two, etc.
for sub_length in range(0, len(nums)+1): backtrack(0, [])
Once we have our output that contains each subset, we will return it.
return output
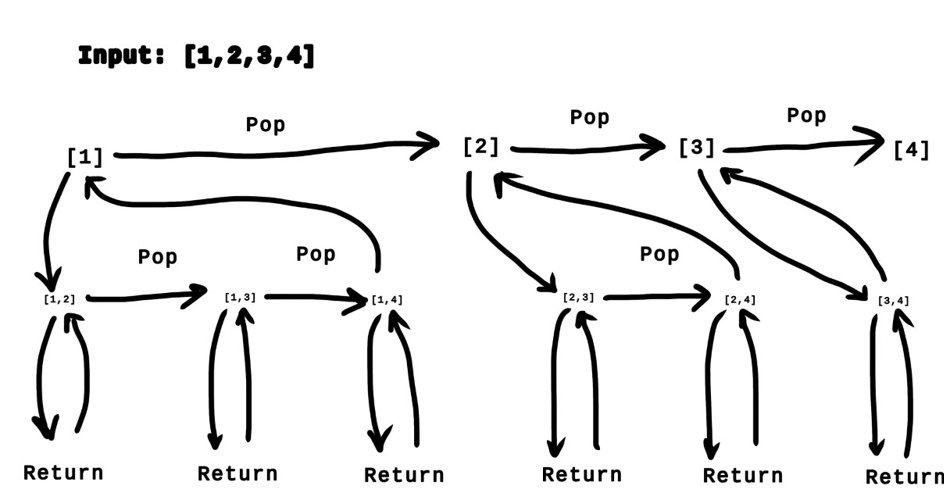
This illustration shows what the flow of the DFS and backtracking would look like within the third iteration where sub_length = 2.