Problem Description
Given an m x n board and a word, find if the word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where "adjacent" cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example 1:
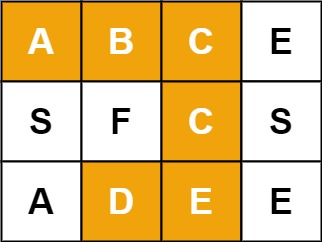
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" Output: true
Example 2:
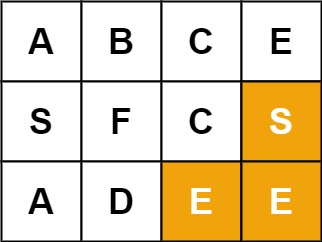
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE" Output: true
Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB" Output: false
Constraints:
m == board.lengthn = board[i].length1 <= m, n <= 2001 <= word.length <= 10^3boardandwordconsists only of lowercase and uppercase English letters.
The description was taken from https://leetcode.com/problems/word-search/.
Problem Solution
#O(N*3^L) Time, O(L) Space where L is Length of Wordclass Solution: def exist(self, board: List[List[str]], word: str) -> bool: for row in range(len(board)): for col in range(len(board[0])): if board[row][col] == word[0] and \ self.dfs(board, row, col, 0, word): return True return False def dfs(self, board:List[List[str]], row:int, col:int, count:int, word:str) -> bool: if count == len(word): return True if not self.in_bounds(board, row, col) or board[row][col] != word[count]: return False temp = board[row][col] board[row][col] = 'seen' found = self.dfs(board, row+1, col, count+1, word) or \ self.dfs(board, row-1, col, count+1, word) or \ self.dfs(board, row, col+1, count+1, word) or \ self.dfs(board, row, col-1, count+1, word) board[row][col] = temp return found def in_bounds(self, board:List[List[str]], row:int, col:int) -> bool: if row < 0 or row >= len(board) or col < 0 or col >= len(board[0]): return False else: return TrueProblem Explanation
If we are looking for a specific path within a matrix or graph, typically a Depth-First Search is more favorable than a Breadth-First Search since that would be more for finding the shortest path or if a path exists from a source to destination.
However, if we were to try and implement a normal Depth-First Search on this problem then that would require tons of space because each path would require its own external memory for tracking whether or not a cell has been visited before.
To avoid that, we can use backtracking.
Backtracking is best for generating each possible combination. We can use it here to generate each possible path.
A general template for backtracking is to first set a base case that checks if the current DFS path leads to a valid solution. If not, check if a placement is valid and if it is then make the placement. Once that placement is made, we'd go down a new DFS path with that placement and if that path didn't lead to a solution or if it did but we need more solutions, we'd backtrack on the choice to make that placement by removing it from the combination. This will free up an opening for another choice, another path.
We can solve this problem by traversing the matrix and if we encounter the first character of the word we're searching for, we will stop and perform a Depth-First Search on that first character. During our DFS, we will follow that backtracking template just mentioned trying each path that the first character leads to and any other consecutive target character after that.
If none of the paths lead to the solution, we will backtrack and mark each cell within the path as unseen so that it is freed up for any later paths to try.
Let's start by traversing each character element within the board by implementing two loops.
The outer loop will traverse the rows and the inner will traverse the columns.
for row in range(len(board)): for col in range(len(board[0])):
We will scan each element within the board and if we come across the first letter of the word we are searching for, we will begin our DFS on that letter with an initial count of zero. If the DFS has successfully found each character within the word then we will return true.
if board[row][col] == word[0] and \ self.dfs(board, row, col, 0, word): return True
If we traversed the entire matrix and didn't find a valid DFS path for the word then we will return false.
return False
Let's make our recursive, dfs function.
For arguments, it will take the board matrix, the row and column coordinates, the count of valid characters we have found within a given DFS path, and the word we are looking for.
It will return whether we found all of the characters in the word.
def dfs(self, board:List[List[str]], row:int, col:int, count:int, word:str) -> bool:
At the beginning of each recursive call, we will first check if we have all of the letters from the word within the current recursive path by comparing the counter to the length of the word.
If they are equal, we will return true.
if count == len(word): return True
If our current element's index is outside the bounds of the board, or if our current element doesn't match the element within the index of the current counter value then we will return false and leave this path.
if not self.in_bounds(board, row, col) or board[row][col] != word[count]: return False
After those checks have been performed, we'll know that we have a good path that contains consecutive letters from the word.
Before we mark the current element as seen, we will need to save the value to a temporary variable so that we can revert it back later. This reverting, or backtracking, is the whole point of this algorithm. This will allow us to circulate each valid character into each position within each DFS path.
temp = board[row][col] board[row][col] = 'seen'
Here is where we will implement our DFS functionality.
We will test the bottom, top, right and left values for a valid path. We will save these path choices to a boolean variable.
found = self.dfs(board, row+1, col, count+1, word) or \ self.dfs(board, row-1, col, count+1, word) or \ self.dfs(board, row, col+1, count+1, word) or \ self.dfs(board, row, col-1, count+1, word)
Once all four directions of a current recursive call have been traveled and its children's recursive calls have traveled as well, we will revert the element back to the temporary value we saved for what it was originally.
We'll do this mainly because we may have duplicate values and if we move down a path that wasn't quite the word we were looking for, then we don't want to ruin the board for a future search.
board[row][col] = temp
At the end of the call, we return whether or not one of our path directions returned true.
return found
Let's also create an in_bounds function we just used within our DFS function to test whether an element's coordinates are within the bounds of the board matrix.
def in_bounds(self, board:List[List[str]], row:int, col:int) -> bool: if row < 0 or row >= len(board) or col < 0 or col >= len(board[0]): return False else: return True
The time and space complexity is a bit complicated for this problem.
Let's think about the DFS as a big snake. If the snake is moving to the right down a valid path then it is not going to go back to its left because that cell was already marked by a parent recursive call. If the snake is moving downward, then it wouldn't move back upward for the same reason. With that being said, an accurate time complexity could be O(N⋅3^L) where N is the number of cells in the matrix and L is the length of the input word.
The time complexity would be the greatest recursive call stack, which is the length of the input word.
Additional Notes
A good way to visualize recursion/DFS is to visualize what each recursive call's child calls are doing.
For example, we chose to travel downward first within the recursive function.
found = self.dfs(board, row+1, col, count+1, word) or \ self.dfs(board, row-1, col, count+1, word) or \ self.dfs(board, row, col+1, count+1, word) or \ self.dfs(board, row, col-1, count+1, word)
That means that the first child call will travel downward first as well before going up, right, or left, and its first child will do the same thing.
That is where the Depth-First Search concept comes into play.