Problem Description
You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
Example 1:
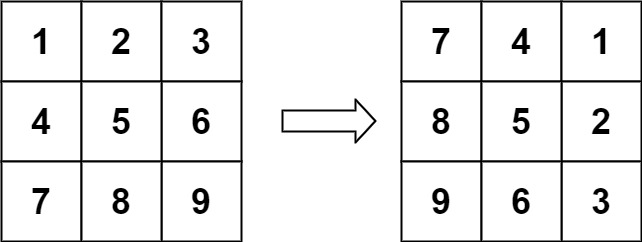
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]] Output: [[7,4,1],[8,5,2],[9,6,3]]
Example 2:
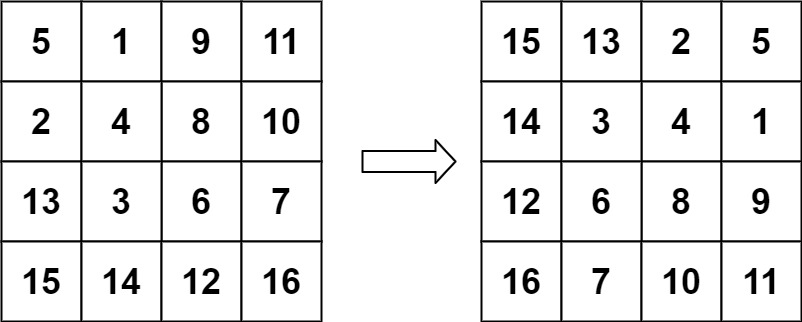
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
Example 3:
Input: matrix = [[1]] Output: [[1]]
Example 4:
Input: matrix = [[1,2],[3,4]] Output: [[3,1],[4,2]]
Constraints:
matrix.length == nmatrix[i].length == n1 <= n <= 20-1000 <= matrix[i][j] <= 1000
The description was taken from https://leetcode.com/problems/rotate-image/.
Problem Solution
#O(N^2) Time, O(1) Spaceclass Solution: def rotate(self, matrix: List[List[int]]) -> None: length = len(matrix[0]) for row in range(length): for col in range(row, length): matrix[col][row], matrix[row][col] = matrix[row][col],matrix[col][row] for i in range(length): matrix[i].reverse()Problem Explanation
Without creating a new matrix, we can solve this problem by transposing the matrix and then reversing each row within the matrix.
What this means is that we are going to swap the elements on the diagonal line going from the top-left border down to the bottom-right border. After that, we will have the reverse image of what we want to output.
Let's take this test case for example :matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
This is what we would like to output.

We will first transpose to flip the image on the diagonal line by swapping each element with the element at its inverse row and column coordinates.
| 5 | 1 | 9 | 11 |
| 2 | 4 | 8 | 10 |
| 13 | 3 | 6 | 7 |
| 15 | 14 | 12 | 16 |
| 5 | 2 | 13 | 15 |
| 1 | 4 | 3 | 14 |
| 9 | 8 | 6 | 12 |
| 11 | 10 | 7 | 16 |
Then, we will reverse each row.
| 15 | 13 | 2 | 5 |
| 14 | 3 | 4 | 1 |
| 12 | 6 | 8 | 9 |
| 16 | 7 | 10 | 11 |
Let's first create a length variable so that we don't have to keep referencing the length later on.
This is an NxN matrix, so this will be the length for both each row and each column.
length = len(matrix[0])
Next, we will make our loops to traverse each element.
We will have an outer loop to traverse each row from top to bottom.
We will also have an inner loop to traverse each column from left to right but with the left bound of the traversal being equal to the current row.
The reason behind this is within each iteration, we are swapping the element at the current row and column with the element at its inverse coordinates. If we were to then visit the element at its inverse coordinates again and swap a second time, then the matrix would be exactly the same as it was originally by the end of our traversal.
By only starting from the column equal to the current row, we can ensure that we are only performing one swap for each of these pairs.
for row in range(length): for col in range(row, length):
As mentioned previously, within each iteration, each element will be swapped with its inverse index.
This means for example, that the element at row two column three will be swapped with the element at row three column two.
This is also why the diagonal values aren't changed because their run and fall values are the same.
matrix[col][row], matrix[row][col] = matrix[row][col], matrix[col][row]
The final thing that we have to do is step through each row in the matrix and reverse the row.
for i in range(length): matrix[i].reverse()